宋代文学家苏轼的作品《八月十五看潮五绝》“万人鼓噪慑吴侬,犹是浮江老阿童。欲识潮头高几许,越山浑在浪花中”,描绘了江潮惊涛骇浪的气势。对海洋波浪的认识与沿海地区人们的活动息息相关,例如捕鱼、晒盐、航行、建造海塘、抵御海洋灾害等,同时浅海波浪也深深地影响着人们的审美文化和日常生活。与海浪相关的波高、波周期、波压力和波轨流速等是设计海岸结构和评估海上作业安全的关键参数。现场观测、实验室实验和数值模拟是获取不同水深对应波高的有效方法。对于现场观测,通常使用海面传感器和近海底压力传感器。与在海面上直接测量相比,使用近海底压力传感器在成本效益和隐蔽性方面具有优势。
线性波理论和谱分析(例如基于近底部高频流速测量的谱分析法和基于风致波浪谱的一般形式的JONSWAP法)是常见的计算波浪参数的方法。其中,简单线性波理论被学术界和工程界广泛使用,是海浪参数估计最经典的理论之一。然而,当只使用特定的统计参数,而不是全波谱时,线性波理论可能导致较大误差。使用普遍的线性波理论从水下压力传感器测量表面波的准确性受到许多研究者的质疑,需要更多的证据来证实线性波理论对不同水深的适用性。从波高或者波压的分布形式上,Rayleigh分布是一种被广泛采用的概率分布模式,是海洋中深水波高的概率密度函数的经典理论,且该理论被修正为单参数Rayleigh分布函数。此外,双参数Weibull分布也用于描述海浪波高分布。目前针对波浪参数的计算缺乏精准且统一的方法,仍存在如下问题:上述三种波浪参数计算方法在浅水和深水环境下都是适用的吗?在从浅水到深水的不同水深环境中,采用线性波模型计算的表面波高误差有何差别、波浪参数统计是否符合Rayleigh或者Weibull分布?为什么采用近海底压力传感器观测的波高常常和海面观测的波高不一致,有什么办法来校正?
近期,汪亚平教授团队基于现场观测数据,通过评估对比多种波浪参数计算方法,比较波参数Rayleigh和Weibull分布的普适性,提出中等水深下显著波高的估算方式,获得了修正线性波理论的无量纲参数及其相应的经验公式,以及从波压力到海面波高的最新校正公式,上述成果发表于海洋学TOP期刊Coastal Engineering和Ocean Engineering等。
研究团队利用海底波浪观测仪器(ADV)获取了从潮滩至中等水深(~ 30米)的一系列波浪观测数据(图1)。研究发现,对于常见的计算波浪参数的方法,不同方法估计的波高、峰值波周期和波轨流速具有较高的一致性,而在浅水站位存在显著差异。另外,还讨论了湍流和床形形态对波致剪应力的影响:在不消除湍流或考虑床形(如波纹)的情况下,波轨流速会被高估或低估。

图1 波浪观测站位. 观测水深为0.8 ~ 27.6米
研究还进一步发现,潮间带的波压力分布形式更符合Weibull分布,表明浅水效应与特定波浪谱和可能的破波或近底湍流有关。随着水深的增加,波压力分布从浅水潮间带的双参数Weibull分布转换到深水区的经典Rayleigh分布。对于沿海工程的应用,提出了一种基于相对水深来更准确地估算显著波高的经验公式(图2):
![]()
在中等水深其接近理论值4,而在极浅水处,测量值比理论值小12.5%。这种显著的减少主要是由于浅水效应,在潮滩上可能存在破波,这使得波谱呈现相对较宽的带状。

图2 不同水深下显著波高的估算公式. kh表示相对水深,Ps代表显著波压力,m0表示0阶矩的 Ps. 不同颜色的符号表示不同水深的观测站位
此外,团队通过先进的观测技术,进一步将水深从30米扩展到超过50米(图3)。利用海表浮标(Spotter/WaveBuoy)以及海底压力传感器(ADV),研究了将压力波转换为表面波的经典线性波理论在不同水深下的有效性阈值。统计分析表明,经典线性波理论在浅水环境中表现较好,但其准确性随着水深的增加而降低。对于沿海工程应用,基于反映浅水的非线性效应的无量纲数(波高与水深的比值),我们提出了通过波压力准确估算表面波(图4)、或者通过表面波估算波压力(图5)的经验公式,将表面波高估计的精度提高至±10%。

图3 波浪观测站位. 观测水深为2.4 ~ 54.8米
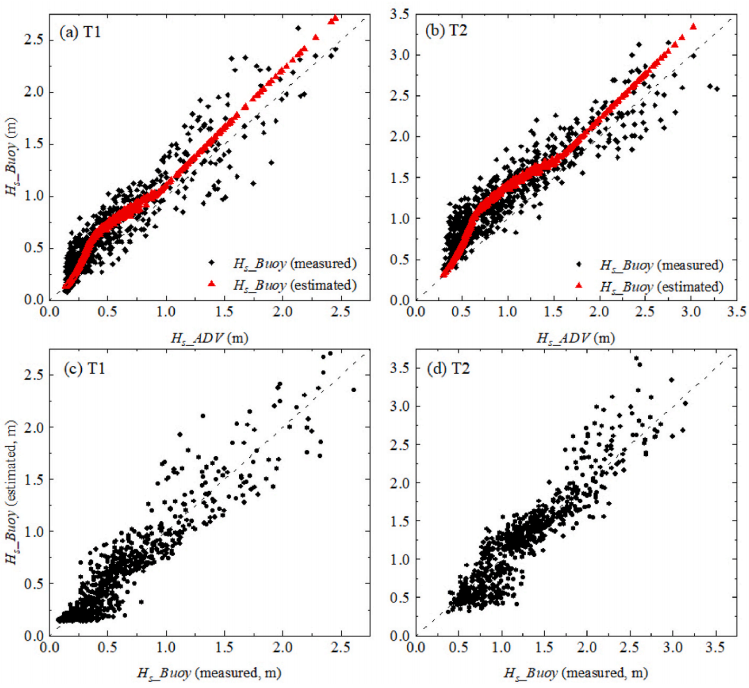
图4 通过波压力(Ps)估算表面波(Hs_Buoy)的经验公式验证. 分别对比两个站位(站位位置见图3)观测值与估算值. 其水深为14.6 ~ 26.0米

图5 通过表面波(Hs_Buoy)估算波压力(Ps)的经验公式验证. 分别对比两个站位(站位位置见图3)观测值与估算值. d表示水深,T代表波周期. 其水深为14.6 ~ 26.0米
参考文献:
Xiong, J., Wang, Y. P., Gao, S., Du, J., Yang, Y., Tang, J., & Gao, J. (2018). On estimation of coastal wave parameters and wave‐induced shear stresses. Limnology and Oceanography: Methods, 16(9), 594-606. doi:10.1002/lom3.10271
Xiong, J., You, Z.-J., Li, J., Gao, S., Wang, Q., & Wang, Y. P. (2020). Variations of wave parameter statistics as influenced by water depth in coastal and inner shelf areas. Coastal Engineering, 159, 103714. doi:10.1016/j.coastaleng.2020.103714
Lu, T., Wang, Y. P., Quan, Q., Gao, C., & Gao, S. (2023). Wave heights from sea surface and bottom measurements: Variations with different water depths. Ocean Engineering, 287. doi:10.1016/j.oceaneng.2023.115848